埃氏筛法

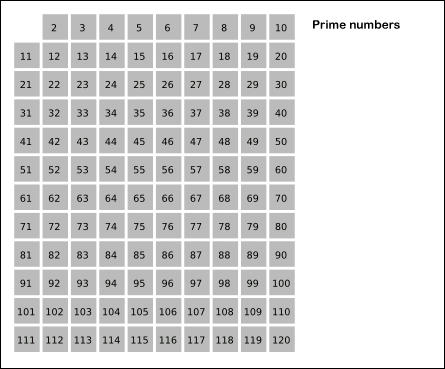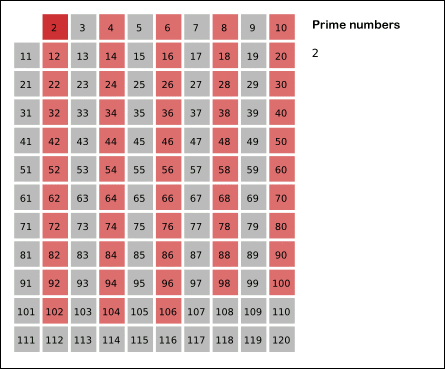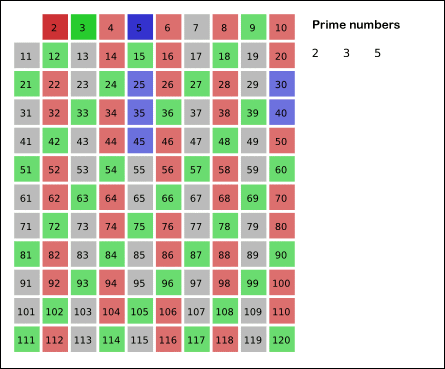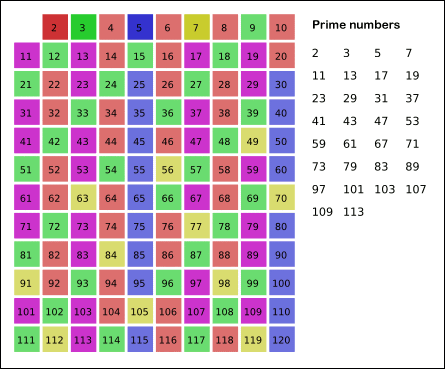
[埃拉托斯特尼]筛法，简称[埃氏筛]或爱氏筛，是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。

原理是从2开始，将每个[素数]的各个倍数，标记成[合数]。一个素数的各个倍数，是一个差为此素数本身的等差数列。此为这个筛法和[试除法]不同的关键之处，后者是以素数来测试每个待测数能否被整除。
此算法时间复杂度为（$nloglog^n$）

整数唯一分解定理

任何一个大于1的[自然数] N,如果N不为[质数]，那么N可以唯一分解成有限个质数的乘积$N=P_1^{a_1}P_2^{a_2}P_3^{a_3}......P_n^{a_n}$，这里$P_1<P_2<P_3......<P_n$均为[质数]，其中指数$a_i$是正整数。

例如：$280=2^3*5^1*7^1$

约数个数定理：

一个大于1的正整数N，那么它的正因数个数为:$(1+a_1)(1+a_2)...(1+a_n)$

约数和定理：

一个大于1的正整数N，那么它的正因素和为：$(p_1^0 + p_1^1 + . . . + p_1^{α1}) . . . (p_k^0 + p_k^1 +​ . . . ​+ p_k^{αk})$